Côté exercice
Exercices calculatoires.
- Calculer la force exercée par la Terre sur le Soleil.
- Calculer la force exercée par la Terre sur la Lune.
- Calculer la force exercée par la Terre sur votre trousse. On prend une masse de 200g pour la trousse. Il faut bien penser à convertir en kg.
- Calculer la force exercée par un stylo sur un autre espacé de 10cm. On prend une masse de 5g pour la trousse. Il faut bien penser à convertir en kg.
| Masse du Soleil : mS = 2,0 × 1030 kg | Masse de la Lune : mL = 7,342 × 1022 kg | Distance Terre-Lune : d = 3 84 000 km |
| Masse de la Terre : mT = 6,0 × 1024 kg | Distance Terre-Soleil : d = 150 × 106 km | R ayon de la Terre : R T = 6400 km |
Correction
Exercices calculatoires.
Calculer la force exercée par la Terre sur le Soleil.
C'est la même valeur que la force exercée par le Soleil sur la Terre.
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {6,0 \times 10^{24} \times 2,0 \times 10^{30}} {(150 \times 10^9)^2} = 3,6 \times 10^{22} N$
Calculer la force exercée par la Terre sur la Lune.
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {6,0 \times 10^{24} \times 7,342 \times 10^{22}} {384000000^2} = 2,0 \times 10^{20} N$
Calculer la force exercée par la Terre sur votre trousse.
mtrousse = 200g = 0,2 kg
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {6,0 \times 10^{24} \times 0,2} {(6400000)^2} = 2 N$
Calculer la force exercée par un stylo sur un autre espacé de 10cm.
mstylo = 5g = 0,005 kg
$F = G \frac {m_A \times m_B} {d^2} = 6,67 \times 10^{-11} \times \frac {0,005 \times 0,005} {(0,1)^2} = 1,7 \times 10^{-13} N$
Cette force est extrêmement faible.
Exercice 10 p 77
Exercice 11 p 77
Exercice 8 p 90
Exercice 11 p 91
a. P = 3,2N
b. $m = \frac P g$
P en N
g en N/kg
m en kg
$m = \frac {3,2} {9,8} = 0,33~kg = 330~g~environ$
Exercice 13 p 91
$g = \frac P m$
P en N
m en kg
g en N/kg
$g = \frac {9990} {900} = 11,1 N/kg$
DNB Blanc p 93
1. a. Le poids est une force et s'exprime en Newton.
b. Le poids P dépend du lieu tout comme l'intensité de la pesanteur g.
c. La masse d'un objet est identique sur la Terre, la Lune et autre endroit. La masse est liée au nombre d'atome. Si le nombre d'atome ne change pas, la masse ne peut pas changer.
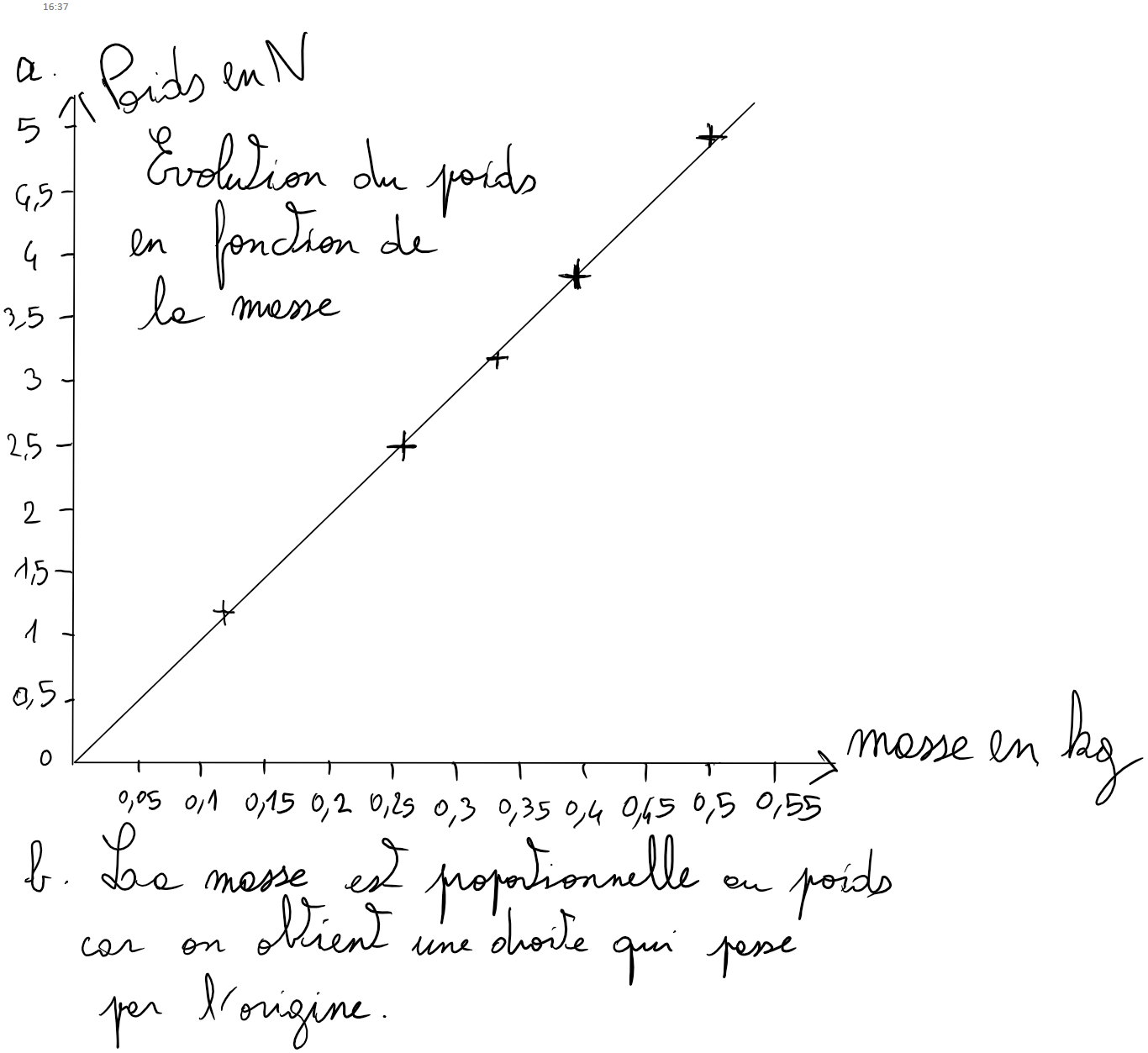
d. Le poids et la masse sont 2 grandeurs proportionnelles :
- sur le graphique P en fonction de la masse, on obtient une droite qui passe par l'origine
- la relation P = m x g avec g constante montre que P est proportionnel à m
e. P = m x g
P en N
m en kg
g en N/kg
P = 1 x 9,8 = 9,8N
2.
P = m x g
P en N
m en kg
g en N/kg
La roche 10057 a une masse m = 919g = 0,919kg
(il faut convertir en kg car la relation P = m x g demande que m soit en kg)
g est celui de la Lune g = 1,6 N/kg
P = 0,919 x 1,6 = 1,5N
3.
P = m x g
P en N
m en kg
g en N/kg
La roche 10057 a une masse m = 919g = 0,919kg quel que soit le lieu
(il faut convertir en kg car la relation P = m x g demande que m soit en kg)
g est celui de la Terre g = 9,8 N/kg
P = 0,919 x 9,8 = 9N
4. a. Point d'application : centre de gravité de la toche
Direction : verticale / droite passant par le centre de la Terre
sens : vers le bas / vers le centre de la Terre
valeur : 9N
b. La flèche a une longueur de 4,5cm. Cela représente 9N.
On cherche à savoir quelle force va être représentée par un segment de 1cm.
| Longueur en cm | Force en N |
|---|---|
| 4,5cm | 9N |
| 1cm | ? |
$\frac {9 \times 1} {4,5} = 2N$
L'échelle est de 1cm pour 2N
5.